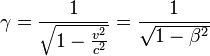| 海外中文网导航 | |||||||||||||||||||||
|
|
|||||||||||||||||||||
|
广义相对论 广义相对性原理认为所有参考系,不论是惯性系还是非惯性系,都同样适合表达自然界定律,但需要用协变张量计算,把自然界定律表示成一个在任意坐标变换下保持不变的数学形式,这条原理又称广义协变原理。据此,物理定律对洛伦兹变换也是协变的。在广义相对论中,为了包括万有引力,时间流逝的速度不仅与物体的运动速度有关,而且还与物体所受到的引力场有关。在引力场较大的地方,如在太阳附近,时间的流逝速度将变慢。 弯曲时空-相对论 爱因斯坦狭义相对论中的内容,他解释了引力作用和加速度作用没有差别的原因。还解释了引力是如何和时空弯曲联系起来的,利用数学,爱因斯坦指出物体使周围空间、时间弯曲,在物体具有很大的相对质量(例如一颗恒星)时,这种弯曲可使从它旁边经过的任何其它事物,即使是光线,也改变路径。广义相对论指出,时空曲率将产生引力。当光线经过一些大质量的天体时,它的路线是弯曲的,这源于它沿着大质量物体所形成的时空曲率。因为黑洞是极大的质量的浓缩,它周围的时空非常弯曲,即使是光线也无法逃逸。 广义相对论认为,由于有物质的存在,空间和时间会发生弯曲,而引力场实际上是一个弯曲的时空。爱因斯坦用太阳引力使空间弯曲的理论,很好地解释了水星近日点进动中一直无法解释的43秒。广义相对论的第二大预言是引力红移,即在强引力场中光谱向红端移动,20年代,天文学家在天文观测中证实了这一点。广义相对论的第三大预言是引力场使光线偏转,。最靠近地球的大引力场是太阳引力场,爱因斯坦预言,遥远的星光如果掠过太阳表面将会发生一点七秒的偏转。1919年,在英国天文学家爱丁顿的鼓动下,英国派出了两支远征队分赴两地观察日全食,经过认真的研究得出最后的结论是:星光在太阳附近的确发生了一点七秒的偏转。 爱因斯坦在1905年既复活了光的微粒说,又维护了麦克斯韦电磁理论的正确性,但是他发觉自己进退维谷。关于辐射的这两个概念是相互矛盾的:如果光是由粒子组成,那么按照万有引力定律,它就会受别的物质影响,果若如此,光速又怎能如狭义相对论要求的那样是绝对恒星呢? 这个矛盾当然应归根于引力。引力在 宇宙中无处不有,并使所有物质加速,而狭义相对论的惯性系是严格地没有加速度的。爱因斯坦很清楚这个症结,并认识到,要使引力能与狭义相对论的电磁时空相协调,首先必须重新理解“力”的概念本身。 牛顿万有引力定律要求一切物体都具有一种称为引力质量的内在属性,用以量度每个物体所能产生的引力。此外,牛顿还用三个基本定律概括了物体在任何力(引力或别的力)作用下的行为。第一定律简单地说就是笛卡儿的惯性原理:不受力的物体保持静止或作匀速直线运动;第二定律规定使一个物体加速的力与物体的加速度和质量都成正比(即人们熟知的公式F=ma);第三定律陈述作用与反作用的平等性:每一个力(例如人推墙的力)都伴之以一个大小相等、方向相反的力(墙也推人)。所以,牛顿的力是使物体偏离其惯性运动的原因。物体总是反抗对其惯性状态的改变,这种反抗由其惯性质量来量度。按照这个思路,万有引力同其他任何力一样,也是一种力,而引力质量之于引力恰如电荷之于电力。 惯性质量相同而带电荷不同的物体在同一电场中受到不同的加速,因而在牛顿理论中就没有理由认为引力质量和惯性质量必定相等。但是,伽利略和牛顿所观察到的引力的基本性质,正是地心引力同样地加速所有物体,而与物体的惯性质量或引力质量、体积以及化学性质都无关。一片羽毛、一个分子或是一块砖,在地球表面附近释放后都同样具有约9.8米/秒的加速度(也就是说,假如没有空气阻力,它们的速度每秒钟都增加9.8米/秒,在第一秒末是9.8米/秒,在第二秒末是19.6米/秒,等等。这个恒定的加速度正是地球表面的引力加速度)。 这意味着,不仅根本不存在“引力中性”的物体,而且所有物体都具有完全一样的相应引力荷。这只有在引力质量与惯性质量严格相等时才可能。这种相等性于是被接受为一条公理,称为等效原理。这种相等起初被认为只是近似的,后来却经受住了整个科学史上最高精度的核查。 匈牙利男爵罗兰•万•厄伍(Lorandvon E6tvbs)先在1889年,后又在1922年对等效原理作了验证,精度达十亿分之一。现在,检验精度已经提高了1000倍。由于一个物体中的所有能量都对惯性质量有贡献(把电子和核束缚在原子中的电磁能就很显然),我们就能得出结论:所有能量都有重量,尤其是,光也有重量。 爱因斯坦意识到,等效原理是理解引力的关键。引力与电磁力大不相同,包括进引力,将给狭义相对论带来实质性的扩充。让我们来进一步考虑等效原理的物理意义。 在爱因斯坦看来,引力质量与惯性的等效只是一个更强得多的等效性的弱形式,而强等效性是把均匀引力和加速统一起来。爱因斯坦指出: 1.任何加速都相当于引力:一个坐在加速度与地心引力(即g=9.8米/秒’)相等的飞船里的人感觉不出与站在地面上有什么区别。 2.引力的作用可以通过选择一个适当的加速参考系来消除。他的著名例子是一架突然断了缆绳的电梯,其中的人将觉得失重,与在太空中已脱离地球引力的人的感觉一样。我们在这里看到引力与自然界所有其他的力(如电力)之间的巨大差异。不可能用加速来冒充电力,因为一个电场中的物体并不受到同样的加速,加速度与物体的电荷有关。准确地说,引力实际上不是一种作用于时空中的不同物体之间的力,而是时空自身的一种性质。引力对人们早已熟悉的时空结构摧毁性地入侵的结果,就是广义相对论。 弯曲时空-新惯性 物理学的自洽性要求一种相对性,即要求参考系中的物理规律能取相同的形式。在这个意义上,广义相对论可说是推翻了狭义相对论。狭义相对论里的参考系都以恒定速度运动,不受力,没有加速度。时空连续体是一种平坦的不毛之地,没有任何局部特征,这种空虚性保证了位置和速度的相对性。但在引力存在的情况下,所有参考系都受到加速。因此在广义相对论中没有普适的惯性参考系。时空连续体变得坑洼不平,而位置和速度只能相对于这样的时空来确定。所有的参考系,无论是惯性系与否,只要我们知道如何从一个参考系正确地过渡到另一个,就能用来描述自然定律。从这个意义上讲,爱因斯坦引力理论的名称是取错了,因为广义相对论的相对性比狭义相对论是减小了。由于一个均匀引力场能由一个加速来消除或代替,并且反之亦然,一个在这个场中下落的物体就不受任何力(人之没有落向地心是因为他脚下地面压力的阻挡)。恒定引力场中的自由下落因而就是物体的“自然”运动。对宇宙中任何一个足够小的区域而言,引力的变化不大,则自由下落运动定义出一个局域惯性参考系,其中的物理定律取其最简单的形式,即由狭义相对论所给出的形式。狭义相对论并没有被完全抛弃,它是被包括到一个更广泛的理论中,而仍保持在一定范围内的适用性。 弯曲时空-宇宙高尔夫球场 时空是弯曲的,可是这个奇怪而又迷人的陈述究竟是什么意思呢?双生子佯谬很好地描绘了狭义相对论时空的刚性结构如何使空间和时间由于观测者的运动而各自改变(收缩或延缓)。广义相对论则完全变革了我们的宇宙观,它断言引力会使整个时空变形。如果在一个给定点上直接的引力效应已被消除,我们仍能测量相邻两点之间的微分效应。在一个缆绳已断掉的电梯里,两个“自由”物体的轨迹在一级近似上是平行的,但实际上两条轨迹线将在6400公里远处的地心相交,因此两轨迹之间就有一个相对加速度(因为它们相互在靠近),对应着一个微分引力场。显示直接引力与微分引力之间区别的一个鲜明事例是海洋潮汐的幅度。虽然太阳对地球表面的直接引力比月亮的强180倍,太阳潮却比月亮潮弱得多。这是因为潮汐并不是由直接引力造成,而是由太阳和月亮对地球上不同点的引力的差异造成。对月亮来说这种差异是6%,而对太阳则只有1.7%。牛顿理论把微分引力效应称作潮汐力。在太阳系里潮汐力是很弱的,而黑洞所产生的潮汐力却能把整个恒星撕碎。然而对广义相对论来说,用潮汐力来描述微分引力是完全多余的,因为这不是一种力学效应而纯粹是一种几何效应。为理解这一点,且看两只开始时沿平行路线滚动且相隔不远的高尔夫球。如果地面完全平坦,它们的轨迹将保持平行,否则它们的相对位置就会改变,一个鼓包会使它们离远,一个凹坑则会使它们靠拢。在宇宙高尔夫球场里,微分引力可以用时空“场地”的弯曲来表示。而且,由于引力总是吸引,这种弯曲就总是凹下而不是隆起。因此,时空弯曲的深刻含义是指由等效原理所造就的引力与几何之间的联系。物体不是在引力迫使下在“平直”时空中运动,而是沿着弯曲时空的恒值线自由地行进。 弯曲时空-弯曲几何 “弯曲”是一个日常用词。三维空间里的欧几里德几何允许我们讲一维的曲线和二维的曲面。圆是一个一维几何图形(只有长度,没有宽度和深度),其半径越短,则弯曲程度越大。反之,如果半径增至无限长,圆就变成了直线,失去了弯曲性。同样地,一个球面随其半径的无限增长也会变成一个平面(若不计地面的粗糙,则在局域尺度上看地球表面是平的)。 弯曲因而是有精确的几何定义的。但当维数增加时,定义变得复杂多了,弯曲程度不能再像圆的情况那样用一个数来描述,而必须讲“曲率”。且看一个简单情况即圆柱面,这是一个二维曲面(图约,平行于其对称轴所量度的曲率为零,而在垂直方向上的曲率则与截出的那个圆相等。 尽管曲率有多重性,仍然可以定义出一个固有曲率。在二维面上的每一个点都可以量出两个相互垂直方向上的弯曲半径,二者乘积的倒数就是曲面的固有曲率。如果两个弯曲半径是在曲面的同一侧,固有曲率就是正的;如果是在两侧,那就是负的。圆柱面的固有曲率为零,事实上它可以被切开平摊在桌面上而不会被扯破,而对一个球面就不可能这样做。 球面、圆柱面及其他任意二维曲面都“包理”在三维欧几里德空间里。这种来自现实生活的具体形象使我们觉得可以区分“内部”和“外部”,并且常说是一个面在空间里弯曲。但是,在纯粹的几何学里,一个二维曲面的性质可以不需要关于包含空间的任何知识而完全确定,更高维的情况也是如此。我们可以描绘四维宇宙的弯曲几何,不需要离开这个宇宙,也不需要参照什么假想的更大空间,且看这是如何做到的。 弯曲空间的数学理论是在19世纪,主要由本哈•黎曼(Bernhard Riemann)发展出来的。即使是最简单的情况,弯曲几何的特性也是欧几里德几何完全没有的。再次考虑一个球面。这是一个二维空间,曲率为正值且均匀(各点都一样),因为两个曲率半径都等于球面的半径。连接球面上两个分离点的最短路线是一个大圆的一段弧,即以球心为中心画在球面上的一个圆的一部分。大圆之于球面正如直线之于平面,二者都是测地线,就是最短长度的曲线。一架不停顿地由巴黎飞往东京的飞机,最省时间的路线是先朝北飞,经过西伯利亚,再朝南飞,这才是最短程路线。由于所有大圆都是同心的,其中任何两个都相交于两点(例如,子午线相交于两极),换句话说,在球面上没有平行的“直线”。 已可看出欧几里德几何是被无情地践踏了。熟知的欧氏几何定律只能应用于没有任何弯曲的平坦空间,一旦有任何弯曲,这些定律就被完全推翻了。球面最明显的几何性质是:与平面上直线的无限延伸不同,如果谁沿着球面上的直线(即沿着大圆)运动,他将总是从相反方向上回到出发点。因此,球面是有限的,或者说封闭的,尽管它没有终极,没有边界(大圆是没有终端的)。球面正是具有任何维数的有限空间的理想原型(由于自转、地形及潮汐等因素,地球表面不是精确的球面,但它同样具有上述性质)。 现在来考查一下负曲率空间的情况。为简单起见,限于二维,典型的例子是双曲面,形如马鞍。如果也沿着这个面上的一条直线运动,一般说来不会再返回出发点,而是无限地远离。像平面一样,双曲面也是开放面,但仅此而已。作为一个曲面,双曲面根本不再是欧几里德型的。大多数曲面并不像球面或双曲面那样具有处处都为正或为负的曲率,而是曲率值逐点变化,正负号在面上不同区域也会改变。 弯曲时空-几何与物质 广义相对论的四维几何。重要的是,时空是弯曲的,而不仅是空间。黎曼曾试图以弯曲空间来使电磁学和引力相和谐,他之所以未成功,是因为没有扭住时间的“脖子”。设想我们把石块掷向地面上10米外的靶子。在地球引力作用下石块将沿连接出手处和靶子的抛物线飞行,其最大高度取决于初始速度。如果石块以10米/秒的速度掷出,并将用1.5秒钟落到目标,则其最大高度为3米。如果改成用枪射击,且子弹初速为500米/秒,则子弹将沿高为0.5毫米的弧线用0.02秒钟击中目标;如果子弹被射到12公里高的空中再落到靶子上(忽略空气的影响和地球自转),它的总飞行时间就大约是100秒。由此推至极限,也可以用速度为3 0公里/秒的光线来射靶子,这时的轨道弯曲变得难以觉察,几乎成了一条直线。显然,所有这些抛物线的曲率半径各不相同。 现在加进时间维度。无论对石块、于弹还是光子,在时空中量度的曲率半径都精确地相等,其值为1光年的星级。因此,更合理的说法是,时空轨道是“直”的,而时空本身被地心引力所弯曲,不受任何其他力的抛射体将沿测地线运动(等价于说沿弯曲几何中的直线运动)。 上面的例子表明时空是怎样在时间上弯曲得比在空间上厉害得多的。一旦所涉及的速度开始增大,时间曲率就变得重要。公路上凸起了一小块,只是空间曲率的一点小小不整齐,一个徒步慢行的人很难觉察到,但对一辆以120公里/小时的速度行驶的汽车来说却很危险,因为它造成时间维度上大得多的变化。 阿瑟•爱丁顿(Arthur Eddington)计算出,l吨的质量放在一个半径为5米的圆中心所造成的空间曲率改变,仅仅影响圆周与直径比值(即欧几里德几何中的…的小数点后第24位。 因此,要给时空造成可观的变化,就得有巨大的质量。地球表面的时空曲率半径如此之大(约1光年,即其自身半径的10亿倍)的事实说明地球的引力场,尽管给物体以98米/秒’的加速度,却是不够强的。对于地球附近的绝大多数物理实验,我们可以继续采用明可夫斯基时空和狭义相对论;欧几里德空间和牛顿力学在涉及的速度较小时也足够精确。 尽管局域地看来似乎平直,我们的宇宙实际上是被物质弄弯曲了。然而,弯曲效应变得明显仅仅是在高度集中的质量附近(例如黑洞),或者是在很大的尺度上(数百万光年,例如研究对象是由数千个星系组成的团)。最近发现的多重类星体是弯曲时空真实性的一个最好证据。一个遥远光源发出的光线沿不同路径穿过弯曲时空,使天文学家看到同一个天体的几个像柔软的光。 弯曲时空-光 狭义相对论时空的刚性结构也像牛顿空间一样被引力的冲击完全破坏了。时空连续体变得柔软了,被它所包含的物质扭曲了,而物质又按照它的弯曲而运动。不过,光线的轨迹仍然是沿着最短路径。这个时空“软体”的结构仍然是由光编织的,广义相对论的本质也仍能由光锥来表示出来。 另一种使弯曲时空及其对物质的影响形象化的有用办法是用一块橡皮片。设想将时空的一部分缩减成二维,且由弹性材料构成。在没有任何别的物体时,橡皮保持平直。如果把一个球放在它上面,它就会变形,凹下一个坑,球的质量越大,凹得就越深。这种似乎是空想的表示方式,可以用所谓镶嵌图来使之具有数学上的严格性。 弯曲时空-爱因斯坦方程 所有理论都有自己的方程式。爱因斯坦引力场方程把时空变形的程度与引力源的性质和运动联系了起来,物质告诉时空必须如河弯曲,而时空告诉物质必须如何运动。爱因斯坦方程是极为复杂的,其中涉及的物理量不再只是力和加速度,而是还有距离和时间间隔。它们是张量,这种量的每一个都像一张有着多项条目的表格,包含着关于几何和物质的所有信息。 引力对物质的作用比电力更为复杂,从而需要有比标量(纯数)和矢量(有三个分量)更复杂的数学术语来进行描述。为认识这一点,我们可回顾在牛顿引力理论中只有物体的引力质量才是引力源,这个质量是由一个固着地联系于物体的纯数来表示的。在爱因斯坦理论中,引力质量只是与物体相联系的总引力量的一个分量。狭义相对论(它对于一个引力可看作均匀的小时空区域总是适用的)已经证明,所有形式的能量都与质量等价,从而都能产生引力。一个物体的能量是与观测者的相对运动有关的。对于一个静止物体,所有的能量都包括在它的“静质量”中(E=thC‘!);但物体一且运动,其动能就会产生质量,从而产生引力。要计算一个物体的引力效应,就必须把它的静止能量与描述其运动的“动量矢量”结合起来,这就是对引力源的完整描述需要使用“能量一动量张量”的缘故。 更有甚者,对时空中的每一点都需要20个数来描述其弯曲情况。时间和空间的几何变形因此需要有“曲率张量”(我们记得,曲率随着维数的增多变得越来越复杂)。爱因斯坦方程正是描述曲率张量与能量一动量张量之间的关系,把二者分别放在一个等式的两边:物质制造曲率,而曲率使物质运动。 并不试图详细讲述爱因斯坦方程。曲率张量和能量一动量张量的不同分量是如此紧密地相互联系着,以至于一般说来不可能找到方程的精确解,甚至不可能从整体上定义什么是空间,什么是时间。我们不得不把引力源加以理想化,才有可能算出一点什么来。有鉴于此,迄今已找到的解(描述着各种弯曲时空)大多与真实的时空毫不相干。在这个意义上,爱因斯坦方程的内涵是太丰富了,它允许无数个有着稀奇古怪性质的理论上的宇宙。 这种丰富性或许损害了爱因斯坦理论的可信性,但是,我们不要由此以为广义相对论只预言那些不可能观测或是超越人类理解力的东西。恰恰相反,爱因斯坦既是一位物理学家,也是一位哲学家,他试图描述我们的这个宇宙,并且从太阳系开始。运用他的方程的近似解,他首先计算出了太阳系里三个不能由牛顿引力定律得出而又可观测的引力效应:太阳附近光线的偏折,水星轨道的异常,引力场中电磁波频率的变小。 除此之外,还有一些自然界存在的情况,其中对引力源所作的简化被证明是完全合理的,相应得出的爱因斯坦方程精确解就能对宇宙的这一部分或那一部分给出很好的描述。看似奇怪的是,这种简化在两个极端的距离尺度上最富成效。我们能够计算真空中一个孤立物体所产生的引力场(也就是该物体周围的时空变形)。一颗恒星的周围区域(例如太阳系)或一个黑洞的附近,都能由这个解来很好地描述,因为这些情况的物质高度集中于一个小时空区域,周围近乎真空。在另一个极端,我们能够计算宇宙整体的平均引力场(宇宙的整体几何),因为在很大的尺度上物质是大致均匀地铺开的,星系就像是均匀的宇宙气体中的分子。广义相对论因而使我们能建立宇宙学,即研究宇宙整体的形状和演化。在相对论天体物理学于70年代出现之前,宇宙学是广义相对论真正得到应用的唯一领域,当然,是和黑洞一起。 广义相对论的第三个主要应用,即引力波,恐怕不得不等到对世纪。爱因斯坦方程在引力理论中的地位,相当于麦克斯韦方程之于电磁学。现在我们都知道电荷的加速产生电磁波,类似地,广义相对论预言引力源的运动也产生波,即曲率的起伏在弹性时空结构中以光速传播。 弯曲时空-检验广义相对论 爱因斯坦提议用来检验广义相对论的三项观测是光线在太阳附近的偏折,水星轨道的异常和引力场中原子谱线的红移。光线经过太阳附近时的偏折结果与爱因斯坦的计算值一致。第二项检验涉及行星运动。按照牛顿天体力学,一个孤立行星是在一个固定的椭圆轨道上围绕太阳运转(椭圆的主轴不动)。由于其他行星的存在,这个运动受到干扰,椭圆轨道会缓慢地进动。1859年,法国天文学家勒维叶发现,水星的近日点(即其轨道上离太阳最近的点)进动得比牛顿理论预期的要快。对外层行星(主要是木星)弓l起的扰动的详细计算得出,水星进动速率应为每百年5514角秒,而实际进动是每百年5557角秒,多出43角秒(一个圆是360“,每一度是3600角秒)。这个异常显然很小(每经过三百万年水星轨道才会比理论值超前一圈),但是牛顿理论在它所运用的领域是如此精确,因而必须对这一现象作出解释。 最自然的设想似乎是还存在一个扰动物体,可能是一个围绕太阳的物质环,或者甚至是一个未知行星。类似的考虑已经使勒维叶成名,他在1846年通过对天王星轨道扰动的分析预言了另一个行星即海王星的存在,随后很快就被证实。勒维叶试图重显辉煌,说是在太阳与水星之间还有一个行星,并取名为火神星。他计算出火神星会很罕见地越过太阳盘面(只有这时才有希望由它投在日面上的阴影来探测它)。但在1877年,刚巧在他预言的火神星超过日面的时间之前,他去世了,因而不会知道自己的失败。那一天所有的望远镜都对着太阳,但是火神星固执地拒不出现。以解释水星近日点进动为唯一目标,出现了许多稍加修改的牛顿式引力理论。当时已经知道,其他行星也有类似的近日点进动,如金星、地球和小行星伊卡鲁斯,但那些能解释一个行星行为的理论却不适用于别的行星。 后来,由于注意到显示近日点进动的是最靠近太阳的那些行星,天文学家开始寻找由太阳内部产生的扰动力。太阳显然不是精确球形的,这种变形原则上能引起近日点进动。然而实际上太阳还是太圆了,牛顿引力理论,无论经过修改与否,仍然被这一小撮古怪行星挫败。 1916年爱因斯坦广义相对论终于为行星近日点进动提供了一个目洽的统一的解释。进动并不是由一种来自太阳的神秘引力所引起,行星是在由太阳质量所弯曲的时空中自由运动。它们的轨道是测地线,而由太阳质量所弯曲的时空连续体的测地线并不是严格的椭圆或双曲线,轨线的轴会随时间而缓慢进动,理论计算的进动速率精确等于观测值爱因斯坦提出的第三项检验是关于光在引力场中的表观“慢化”。电磁辐射的频率减小,波长相应地增大,即所谓“红化”(红光在可见光谱中波长最长)。要以现有的实验精度来检验广义相对论,太阳上的这种效应就太微弱了,即使是密度比太阳大得多,能给光线施加更强束缚力的恒星,由于其光谱受磁场和星体内部物质不明运动的影响很大,因而很难把各种效应区分开来。 这第三项检验简单地就是引力场中时间弹性的另一种说法。狭义相对论已经证明,加速使钟变慢(双生子佯谬)。按照等效原理,就可以得出结论,引力也会使钟变慢:一楼的钟就会走得比二楼的钟慢。直到爱因斯坦逝世以后,才能造出足够精确的钟来测量地球这样弱的引力场中的时间弹性。 1960年,哈佛大学的物理学家以千分之一的精度测出了沿垂向下落23米的伽玛射线的频率移动(伽玛射线是一种高能电磁辐射)。观测太阳附近光线的偏折必须等日食到来,检验水星近日点是否进动得太快需要一个世纪的观测资料积累,而现在有了可按设计重复进行的实验室测量。一个繁荣的实验引力时代开始了。从1976年起,超稳定即精确度为一千万亿分之一的钟被放到了高空飞机上,那里的引力比地面上减弱的程度应当可以测量出来。这种飞行的电磁钟与在地面实验室里同样的钟作了比较。二者的速率确有差别,而且与广义相对论预言的结果完全一致。空间探测器的出现使得测量太阳引力场更显著一些的时间弹性效应成为可能。用雷达发射器向位于太阳另一侧的一个空间探测器发出一个无线电讯号,讯号被探测器反射并返回地球,全程的时间在地球上记量,被太阳引力变曲的几何使得这个时间与讯号在平坦真空中传播的时间不同。这个实验是在1971年用水手号探测器进行的,它再次证实了时间延迟效应。 也许有人要问,为什么要做这么多很花钱的实验去证实一个看来已经很好的理论?回答是,所有这些广义相对论实验都只涉及太阳系的引力场,而这个场是处处都很弱的,也是定常态的(即不随时间变化)。这个繁荣的实验引力时代激发了理论家们的想象,许多引力理论被提出来与爱因斯坦理论竞争。那些理论大多含有一些附加参量,可以由发明者随意调节。这类理论中最著名的一个是由德国物理学家帕索•约丹(PascualJordan)和法国物理学家叶维•舍里(Yves Thir对提出,后来由美国物理学家卡尔•布兰斯(Carl Brans)和罗伯特•迪克(Robert Dick)所发展的(迪克本人对实验引力的发展有着卓越的贡献)。由于附加参量的灵活性,那些理论可以被调节得能说明太阳系里观测到的所有效应。 那么,怎么能确定究竟那一个理论是正确的呢? 只有通过分析所有这些理论对强的、动态的(即随时间迅速变化)引力场情况所作的预测,才得作出回答。然而在相当长的时期里,自然界并未给我们提供合适的检验场所,直到1974年双脉冲星的发现,情况才有大变。这两个靠得很近且相互绕转的中子星的轨道周期在变短,观测结果与爱因斯坦理论一致,而与所有其他参与竞争的理论都不相符。 弯曲时空-理论的魅力 广义相对论无疑是人类有史以来最辉煌的智力业绩之一,而且是由一个人单独完成的。 1911年,在布拉格大学工作的爱因斯坦首次计算了光线在引力场中的偏折。他的结果本应在1914年日食时检验,但是第一次世界大战的爆发使这个计划搁浅。这对爱因斯坦来说倒是幸运的,因为他的理论在当时还不成熟,他的预测是错的。然而,他没有因挫折而丧气,他承认自己是一个科学上的“偏执狂”。英国物理学家泡尔•狄拉克(Paul Dirac)后来说道:“科学完全占据了爱因斯坦的思维。如果他给你一杯茶,当你在用匙搅动时,他就会在思考如何对杯中茶叶的运动作出科学解释。” 爱因斯坦于1915年11月完善了他的广义相对论方程,并陆续于11月4日、11日、18日和25日在《柏林报告》(BerlinerBench比)上发表,他的理论从此走上了灿烂的历程。最早的两本有关专著于1918年出版,一本是在伦敦,作者是阿瑟•爱丁顿(那时,德国科学在英国受到冷遇,英国图书馆不再接收德国期刊。爱丁顿读到的爱因斯坦论文,是他的一个德国朋友邮寄的,可能是英国仅有的一份);另一本是在柏林,由赫曼•魏尔出ermann We 周写成。光线经过太阳附近时的偏折,是1919年5月29日日食时在巴西的索布拉尔观测到的,这应感谢弗兰克•戴森(Frank Dvson)和爱丁顿的热忱。对爱因斯坦预言的证实是皇家学会于1919年间月6日在伦敦举行的一次著名会议上宣布的。 那时,第一次世界大战刚刚结束。整个世界恶梦初醒、疲惫不堪,而又在寻求着新的理想。爱因斯坦理论以其关于弯曲空间的稀奇思想抓住了公众的想象,尽管一般人连其中的一个字都不懂。无数的科普文章出现在通俗的和专业的期刊上,人们都被迷住了,相对论成了时髦的话题。爱因斯坦成了世界上最负盛名的思想家,无论是什么方面的问题,都有人去问他的观点。美国以隆重的仪式欢迎了他,他成了公众的偶像科学界的反应就复杂得多。有的人为爱因斯坦独行侠式的创造所倾倒,赞美之词超过以前之于牛顿。“思辨威力的一个最美妙的例证”,赫曼•魏尔这样宣称,并且又毫不犹豫地加上:“遮掩真理的墙已被推倒”。马克斯•玻恩(Max Born)则在1955年说是“人类智慧最伟大的成就”。值得强调的是,在物理学家中,对广义相对论最强烈支持的是那些能够理解它的人。 另一方面,那些拒不接受这个理论的人也是太过分了。很难不提一位物理学家波阿色(H•Bouasse)的令人惊讶的评论:“这种在我看来将是短命的赞誉,是由于爱因斯坦理论不属于物理理论的范畴,它是一种先验的、凌驾于一切之上的、不可理解的假设,给它的成功予以模棱两可的理由……最后,我们实验物理学家要说的是:我们只接受那些适合我们的理论,我们拒绝那些我们不能理解因而对我们无用的理论。” 广义相对论的另一个激烈反对者阿尔瓦•古尔斯胜(AllvarGullstrand),是瑞典的眼科学家和数学家,1911年诺贝尔生理学奖获得者,也是诺贝尔物理学奖委员会成员。这或许就是为什么1921年授予爱因斯坦诺贝尔奖是“特别由于他对支配光电效应的定律的发现”,而不是由于他的相对论。 法国物理学家约翰•爱森斯塔(Jean Eisenstaedt)评论道:“这种偏见就像正派的绅士们憎恨本世纪产生的立体派、非图形派和达达派绘画。那些纳土们庆贺自己不懂新艺术,而嘲笑表示赞扬的人是不懂装懂的假内行。”这里,对科学和艺术创造二者的对照是恰当的。广义相对论常被比作一项优美的抽象艺术创作,然而一个理论的优美并不保证它的正确,注重实用的物理学家需要时间来确认它符合自己的原则。国际天文学联合会(它每三年举行一次全世界天文学家的大会)于1922年热情地设立了一个“相对论”委员会,它只开过一次会,然后就决定再继续活动是无益的。 时至今日,论争仍未结束。然而相对论是在发展壮大,尤其是在过去的近30年里,其起因则是来自奇特的遥远星球的闪烁信号首次进入了大型射电望远镜。 弯曲时空-虫洞 60多年前,阿尔伯特·爱因斯坦提出了“虫洞”理论。那么,“虫洞”是什么呢?简单地说,“虫洞”是连接宇宙遥远区域间的时空细管。它可以把平行宇宙和婴儿宇宙连接起来,并提供时间旅行的可能性。 早在20世纪50年代,已有科学家对“虫洞”作过研究,由于当时历史条件所限,一些物理学家认为,理论上也许可以使用“虫洞”,但“虫洞”的引力过大,会毁灭所有进入的东西,因此不可能用在宇宙航行上。 随着科学技术的发展,新的研究发现,“虫洞”的超强力场可以通过“负质量”来中和,达到稳定“虫洞”能量场的作用。科学家认为,相对于产生能量的“正物质”,“反物质”也拥有“负质量”,可以吸去周围所有能量。像“虫洞”一样,“负质量”也曾被认为只存在于理论之中。不过,目前世界上的许多实验室已经成功地证明了“负质量”能存在于现实世界,并且通过航天器在太空中捕捉到了微量的“负质量”。 据美国华盛顿大学物理系研究人员的计算,“负质量”可以用来控制“虫洞”。他们指出,“负质量”能扩大原本细小的“虫洞”,使它们足以让太空飞船穿过。他们的研究结果引起了各国航天部门的极大兴趣,许多国家已考虑拨款资助“虫洞”研究,希望“虫洞”能实际用在太空航行上。 宇航学家认为,“虫洞”的研究虽然刚刚起步,但是它潜在的回报,不容忽视。科学家认为,如果研究成功,人类可能需要重新估计自己在宇宙中的角色和位置。现在,人类被“困”在地球上,要航行到最近的一个星系,动辄需要数百年时间,是目前人类不可能办到的。但是,未来的太空航行如使用“虫洞”,那么一瞬间就能到达宇宙中遥远的地方。 据科学家观测,宇宙中充斥着数以百万计的“虫洞”,但很少有直径超过10万公里的,而这个宽度正是太空飞船安全航行的最低要求。“负质量”的发现为利用“虫洞”创造了新的契机,可以使用它去扩大和稳定细小的“虫洞”。 科学家指出,如果把“负质量”传送到“虫洞”中,把“虫洞”打开,并强化它的结构,使其稳定,就可以使太空飞船通过。 虫洞的概念最初产生于对史瓦西解的研究中。物理学家在分析白洞解的时候,通过一个阿尔伯特·爱因斯坦的思想实验,发现宇宙时空自身可以不是平坦的。如果恒星形成了黑洞,那么时空在史瓦西半径,也就是视界的地方与原来的时空垂直。在不平坦的宇宙时空中,这种结构就意味着黑洞视界内的部分会与宇宙的另一个部分相结合,然后在那里产生一个洞。这个洞可以是黑洞,也可以是白洞。而这个弯曲的视界,就叫做史瓦西喉,它就是一种特定的虫洞。 自从在史瓦西解中发现了虫洞,物理学家们就开始对虫洞的性质发生了兴趣。 虫洞连接黑洞和白洞,在黑洞与白洞之间传送物质。在这里,虫洞成为一个阿尔伯特·爱因斯坦—罗森桥,物质在黑洞的奇点处被完全瓦解为基本粒子,然后通过这个虫洞(即阿尔伯特·爱因斯坦—罗森桥)被传送到白洞并且被辐射出去。 虫洞还可以在宇宙的正常时空中显现,成为一个突然出现的超时空管道。 虫洞没有视界,它只有一个和外界的分界面,虫洞通过这个分界面进行超时空连接。虫洞与黑洞、白洞的接口是一个时空管道和两个时空闭合区的连接,在这里时空曲率并不是无限大,因而我们可以安全地通过虫洞,而不被巨大的引力摧毁。理论推出的虫洞还有许多特性,限于篇幅,这里不再赘述。 黑洞、白洞、虫洞仍然是目前宇宙学中“时空与引力篇章”的悬而未解之谜。黑洞是否真实存在,科学家们也只是得到了一些间接的旁证。当前的观测及理论也给天文学和物理学提出了许多新问题,例如,一颗能形成黑洞的冷恒星,当它坍缩时,其密度已然会超过原子核、核子、中子……,如果再继续坍缩下去,中子也可能被压碎。那么,黑洞中的物质基元究竟是什么呢?有什么斥力与引力对抗才使黑洞停留在某一阶段而不再继续坍缩呢?如果没有斥力,那么黑洞将无限地坍缩下去,直到体积无穷小,密度无穷大,内部压力也无穷大,而这却是物理学理论所不允许的。 总之,目前我们对黑洞、白洞和虫洞的本质了解还很少,它们还是神秘的东西,很多问题仍需要进一步探讨。目前天文学家已经间接地找到了黑洞,但白洞、虫洞并未真正发现,还只是一个经常出现在科幻作品中的理论名词。 虫洞也是霍金构想的宇宙期存在的一种极细微的洞穴。美国科学家对此做了深入的研究。目前的宇宙中,“宇宙项”几乎为零。所谓的宇宙项也称为“真空的能量”,在没有物质的空间中,能量也同样存在其内部,这是由爱因斯坦所导入的。宇宙初期的膨胀宇宙,宇宙项是必须的,而且,在基本粒子论里,也认为真空中的能量是自然呈现的。那么,为何目前宇宙的宇宙项变为零呢?柯尔曼说明:在爆炸以前的初期宇宙中,虫洞连接着很多的宇宙,很巧妙地将宇宙项的大小调整为零。结果,由一个宇宙可能产生另一个宇宙,而且,宇宙中也有可能有无数个这种微细的洞穴,它们可通往一个宇宙的过去及未来,或其他的宇宙。 旋转的或带有电荷的黑洞内部连接一个相应的白洞,你可以跳进黑洞而从白洞中跳出来。这样的黑洞和白洞的组合叫做虫洞。 最后,即使虫洞存在并且是稳定的,穿过它们也是十分不愉快的。贯穿虫洞的辐射(来自附近的恒星,宇宙的微波背景等等)将蓝移到非常高的频率。当你试着穿越虫洞时,你将被这些X射线和伽玛射线烤焦。虫洞的出现,几乎何以说是和黑洞同时的。 物理学家一直认为,虫洞的引力过大,会毁灭所有进入它的东西,因此不可能用在宇宙旅行之上 。但是,假设宇宙中有虫洞这种物质存在,那么就可以有一种说法:如果你于12:00站在虫洞的一端(入口),那你就会于12:00从虫洞的另一端(出口)出来。 黑洞和黑洞之间也可以通过虫洞连接,当然,这种连接无论是如何的将强,它还是仅仅是一个连通的“宇宙监狱”。 虫洞有几种说法 一是空间的隧道,就像一个球,你要沿球面走就远了但如果你走的是球里的一条直径就近了,虫洞就是直径 二是黑洞与白洞的联系 三是你说的时间隧道,根据爱因斯坦所说的你可以进行时间旅行,但你只能看,就像看电影,却无法改变发生的事情,因为时间是线行的,事件就是一个个珠子已经穿好,你无法改变珠子也无法调动顺序 到现在为止,我们讨论的都是普通“完美”黑洞。细节上,我们讨论的黑洞都不旋转也没有电荷。如果我们考虑黑洞旋转同时/或者带有电荷,事情会变的更复杂。特别的是,你有可能跳进这样的黑洞而不撞到奇点。结果是,旋转的或带有电荷的黑洞内部连接一个相应的白洞,你可以跳进黑洞而从白洞中跳出来。这样的黑洞和白洞的组合叫做虫洞。 白洞有可能离黑洞十分远;实际上它甚至有可能在一个“不同的宇宙”--那就是,一个时空区域,除了虫洞本身,完全和我们在的区域没有连接。一个位置方便的虫洞会给我们一个方便和快捷的方法去旅行很长一段距离,甚至旅行到另一个宇宙。或许虫洞的出口停在过去,这样你可以通过它而逆着时间旅行。总的来说,它们听起来很酷。 但在你认定那个理论正确而打算去寻找它们之前,你因该知道两件事。首先,虫洞几乎可以肯定不存在。正如我们上面我们说到白洞时,只因为它们是方程组有效的数学解并不表明它们在自然中存在。特别的,当黑洞由普通物质坍塌形成(包括我们认为存在的所有黑洞)并不会形成虫洞。如果你掉进其中的一个,你并不会从什么地方跳出来。你会撞到奇点,那是你唯一可去的地方。 还有,即使形成了一个虫洞,它也被认为是不稳定的。即使是很小的扰动(包括你尝试穿过它的扰动)都会导致它坍塌。 即使虫洞存在并且是稳定的,穿过它们也是十分不愉快的。贯穿虫洞的辐射(来自附近的恒星,宇宙的微波背景等等)将蓝移到非常高的频率。当你试着穿越虫洞时,你将被这些X射线和伽玛射线烤焦。虫洞的出现,几乎何以说是和黑洞同时的。 在史瓦西发现了史瓦西黑洞以后,理论物理学家们对爱因斯坦常方程的史瓦西解进行了几乎半个世纪的探索。包括上面说过的克尔解、雷斯勒——诺斯特朗姆解以及后来的纽曼解,都是围绕史瓦西的解研究出来的成果。我在这里将介绍给大家的虫洞,也是史瓦西的后代。 虫洞在史瓦西解中第一次出现,是当物理学家们想到了白洞的时候。他们通过一个爱因斯坦的思想实验,发现时空可以不是平坦的,而是弯曲的。在这种情况下,我们会十分的发现,如果恒星形成了黑洞,那么时空在史瓦西半径,也就是视界的地方是与原来的时空完全垂直的。在不是平坦的宇宙时空中,这种结构就以为着黑洞的视界内的部分会与宇宙的另一个部分相结合,然后在那里产生一个洞。这个洞可以是黑洞,也可以是白洞。而这个弯曲的视界,叫史瓦西喉,也就是一种特定的虫洞。 自从在史瓦西解中发现了虫洞,物理学家们就开始对虫洞的性质感到好奇。 我们先来看一个虫洞的经典作用:连接黑洞和白洞,成为一个爱因斯坦——罗森桥,将物质在黑洞的奇点处被完全瓦解为基本粒子,然后通过这个虫洞(即爱因斯坦——罗森桥)被传送到这个白洞的所在,并且被辐射出去。 当然,前面说的仅仅是虫洞作为一个黑洞和白洞之间传送物质的道路,但是虫洞的作用远不只如此。 黑洞和黑洞之间也可以通过虫洞连接,当然,这种连接无论是如何的将强,它还是仅仅是一个连通的“宇宙监狱”。 虫洞不仅可以作为一个连接洞的工具,它还开宇宙的正常时空中出现,成为一个突然出现在宇宙中的超空间管道。 虫洞没有视界,踏有的仅仅是一个和外界的分解面。虫洞通过这个分解面和超空间连接,但是在这里时空曲率不是无限大。就好比在一个在平面中一条曲线和另一条曲线相切,在虫洞的问题中,它就好比是一个四维管道和一个三维的空间相切,在这里时空曲率不是无限大。因而我们现在可以安全地通过虫洞,而不被巨大的引力所摧毁。 那么虫洞都有些什么性质呢? 利用相对论在不考虑一些量子效应和除引力以外的任何能量的时候,我们得到了一些十分简单、基本的关于虫洞的描述。这些描述十分重要,但是由于我们研究的重要是黑洞,而不是宇宙中的洞,因此我在这里只简单介绍一下虫洞的性质,而对于一些相关的理论以及这些理论的描述,这里先不涉及。 虫洞有些什么性质呢?最主要的一个,是相对论中描述的,用来作为宇宙中的告诉火车。但是,虫洞的第二个重要的性质,也就是量子理论告诉我们的东西又明确的告诉我们:虫洞不可能成为一个宇宙的告诉火车。虫洞的存在,依赖于一种奇异的性质和物质,而这种奇异的性质,就是负能量。只有负能量才可以维持虫洞的存在,保持虫洞与外界时空的分解面持续打开。当然,狄拉克在芬克尔斯坦参照系的基础上,发现了参照系的选择可以帮助我们更容易或者难地来分析物理问题。同样的,负能量在狄拉克的另一个参照系中,是非常容易实现的,因为能量的表现形式和观测物体的速度有关。这个结论在膜规范理论中同样起到了十分重要的作用。根据参照系的不同,负能量是十分容易实现的。在物体以近光速接近虫洞的时候,在虫洞的周围的能量自然就成为了负的。因而以接近光速的速度可以进入虫洞,而速度离光速太大,那么物体是无论如何也不可能进入虫洞的。这个也就是虫洞的特殊性质之一。 但是虫洞并没有这么太平。前面说的是在安静的相对论中的虫洞,在暴躁的量子理论中,虫洞的性质又有了十分重要的变化。 我们先来看在黑洞中的虫洞,也就是史瓦西喉和奇点周围形成的子宇宙。 黑洞周围的量子真空涨落在黑洞巨大引力的作用下,会被黑洞的引力能“喂”大,成为十分的能量辐射。这种能量会毫不留情地将一切形式的虫洞摧毁。 在没有黑洞包围的虫洞中,由于同样的没有黑洞巨大引力的“喂养”,虫洞本身也不可能开启太久。虫洞有很大几率被随机打开,但是有更大的几率突然消失。虫洞打开的时间十分短,仅仅是几个普朗克时间。在如此短的“寿命”中,即使是光也不可能走完虫洞的一半旅途,而在半路由于虫洞的消失而在整个时空中消失,成为真正的四维时空组旅行者。 而且,在没有物体通过虫洞的时候,虫洞还比较“长寿”,而一旦有物体进入了虫洞,如果这个物体是负能量的,那么还好,虫洞会被撑开;但是如果物体是正能量的,那么虫洞会在自己“自然死亡”以前就“灭亡”掉。而在宇宙中,几乎无时无刻不存在能量辐射通过宇宙的每一个角落,而这些辐射都是正能量的,因此几乎可以肯定,在自然情况下是不存在虫洞的。 旋转的或带有电荷的黑洞内部连接一个相应的白洞,你可以跳进黑洞而从白洞中跳出来。这样的黑洞和白洞的组合叫做虫洞。 虫洞不仅可以作为一个连接洞的工具,它还开宇宙的正常时空中出现,成为一个突然出现在宇宙中的超空间管道。 虫洞没有视界,踏有的仅仅是一个和外界的分解面。虫洞通过这个分解面和超空间连接,但是在这里时空曲率不是无限大。就好比在一个在平面中一条曲线和另一条曲线相切,在虫洞的问题中,它就好比是一个四维管道和一个三维的空间相切,在这里时空曲率不是无限大。因而我们现在可以安全地通过虫洞,而不被巨大的引力所摧毁。 黑洞周围的量子真空涨落在黑洞巨大引力的作用下,会被黑洞的引力能“喂”大,成为十分的能量辐射。这种能量会毫不留情地将一切形式的虫洞摧毁。 在没有黑洞包围的虫洞中,由于同样的没有黑洞巨大引力的“喂养”,虫洞本身也不可能开启太久。虫洞有很大几率被随机打开,但是有更大的几率突然消失。虫洞打开的时间十分短,仅仅是几个普朗克时间。在如此短的“寿命”中,即使是光也不可能走完虫洞的一半旅途,而在半路由于虫洞的消失而在整个时空中消失,成为真正的四维时空组旅行者。 而且,在没有物体通过虫洞的时候,虫洞还比较“长寿”,而一旦有物体进入了虫洞,如果这个物体是负能量的,那么还好,虫洞会被撑开;但是如果物体是正能量的,那么虫洞会在自己“自然死亡”以前就“灭亡”掉。而在宇宙中,几乎无时无刻不存在能量辐射通过宇宙的每一个角落,而这些辐射都是正能量的,因此几乎可以肯定,在自然情况下是不存在虫洞的。 虫洞的自然产生机制有两种: 其一,是黑洞的强大引力能; 其二,是克尔黑洞的快速旋转,其伦斯——梯林效应将黑洞周围的能层中的时空撕开一些小口子。这些小口子在引力能和旋转能的作用下被击穿,成为一些十分小的虫洞。这些虫洞在黑洞引力能的作用下,可以确定它们的出口在那里,但是现在还不可能完全完成,因为量子理论和相对论还没有完全结合。 弯曲时空-在弯曲时空中遇上大危机在宇宙的深处,艾弗拉德到他的宇宙飞船外去修理一支故障的天线。他注意到远处星球的美丽星光看来有点扭曲,彷佛是透过厚厚的透镜所观察到的,并感觉到有股力量在轻扯他的全身。他大概猜到这是怎么回事,便从多用途腰带取下一支雷射笔和一罐刮胡膏,接着启动喷射背包,开始检验他的想法。 弯曲时空-太空游泳威斯登现象到底是如何运作的?像艾弗拉德这样的探险家,要怎样在太空中游泳呢?平直空间中的孤立系统(例如航天员加上失去动力的喷射背包),其质心是绝对不会加速的。假如艾弗拉德在背包上绑一条绳子,接着把背包猛抛出去,再收回来,那么在整个抛收过程中,尽管喷射背包和航天员先是互相远离,之后又重聚,两者的整体质心却是一直不变的。最后,他和喷射背包会回到起初的位置。更简单地说,艾弗拉德无法仅靠反复改变(及复原)形状或结构,就能移动。 http://a1.att.hudong.com/29/33/01200000012881118753333179329_s.jpg
|
|||||||||||||||||||||
|
1915年6,7月,爱因斯坦在阿廷根作了6次关于广义相对论的学术报告。同年11月提出广义相对论引力方程的完整形式,并且成功地解释了水星近日点运动。 1916年,3月他完成总结性论文《广义相对论的基础》, 广义相对论正式地出炉了!值得指出的是,数学家希尔伯特在爱因斯坦之前就推出了引力场方程,他说:“哥廷根大街的每一个小孩都比爱因斯坦更懂四维几何,但发明广义相对论的是爱因斯坦而不是数学家。”
爱因斯坦方程是天人合一的典范,它的出世,表明纯粹理性具有非凡美感,人类心智,极富荣耀。
G-ab=T-ab (3) 在真空情景下,爱因斯坦方程可以写成: R-ab=0 (4) 在有些情景下,人们处理带有宇宙项的爱因斯坦方程。
爱因斯坦方程(3)的思想精髓众所周知:物质等于时空的弯曲。这一点是最重要的,如果问爱因斯坦理论最震撼人心的思想是什么,一半人会回答是等效原理,另外一半人会回答是物质等于时空的弯曲。真正思考过这个问题的人,多数会选择后者。这个后者,也被很多研究圈量子引力的人最喜欢的,他们把这个叫做“背景无关性”。可以相信,一个正确的量子引力理论,它肯定不需要事先假定理论适用的背景。
|
|||||||||||||||||||||
| 在电动力学里,由于电磁波传播于真空的速度是有限的,观测者探测到电磁波的时间,会不同于这电磁波发射的时间,称为推迟时间。
根据麦克斯韦方程组,电磁波传播于真空的速度是光速
因此,可以定义推迟时间为
推迟时间的概念意味着电磁波的传播不是瞬时的。电磁波从发射位置传播到终点位置,需要一段传播期间,称为时间延迟。与日常生活的速度来比,电磁波传播的速度相当快。因此,对于小尺寸系统,这时间延迟,通常很难被注意到。例如,从开启电灯泡到这电灯泡的光波抵达到观测者的双眼,所经过的时间延迟,只有几兆分之一秒。但是,对于大尺寸系统,像太阳照射阳光到地球,时间延迟大约为 8 分钟,比较能够被观测到。
|
|||||||||||||||||||||
|
【题目】洛伦兹变换与狭义相对论在理论上的本质区别 【摘要】通过追溯了洛伦兹因子(Lorentz factor)的起源,指出洛伦兹变换(Lorentz transformation)与狭义相对论在理论上有本质的区别--“以太”(ether)观的不同。 【关键词】洛伦兹因子(Lorentz factor),洛伦兹变换(Lorentz transformation),狭义相对论(Special relativity),“以太”(ether) 【引言】洛伦兹因子是一个出现在狭义相对论中的速记因子,它代表了相对论的效应。狭义相对论的关键点之一是对对洛伦兹因子(Lorentz factor)的认识。由此,必须清楚洛伦兹因子(Lorentz factor)的起源。 【正文】 洛伦兹因子是一个出现在狭义相对论中的速记因子,它代表了相对论的效应:
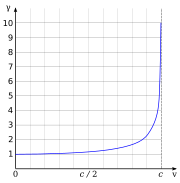
其中β代表了v/c,即物体速度与光速的比值。 洛伦兹因子与速度的关系。速度为零时洛伦兹因子为1,速度趋于时洛伦兹因子趋于无穷大。
非相对论性条件:当速度远小于光速(非相对论性条件下),即,则β趋近于0,而γ趋近于1,回到传统的牛顿力学描述。 荷兰物理学家洛伦兹(劳仑兹)(Hendrik Lorentz)一生实际是以“以太”理论(Lorentz Ether theory) 而闻名于世,他根据自己的理论,理论性地解释了塞曼效应(Zeeman effect),因此而获得1902年物理学诺贝尔奖。 洛伦兹因子的起源 在1892-1895年期间,洛伦兹最初的理论是基于“以太”(ether)静止[1],但他的这个理论解释不了“以太漂移实验”(aether drift experiments),因此,洛伦兹引入了以“v/c”作为“当地时间”(local time)的概念来将运动的“以太”和静止的“以太”联系起来,其公式是“t' = t − vx / c2 ”,其中,“t”表示观察者静止于“以太”中的时间,而“t'”表示观察者和“以太”一起运动时的时间。其数学方法就是洛伦兹因子(Lorentz factor)的起源。。(注:local time t' = t − vx / c2, where t is the time coordinate for an observer resting in the ether, and t' is the time coordinate for an observer moving in the ether.)[2] 洛伦兹因子的形成过程 1879年,麦克斯韦在一封信中指出:“地面上测量光速的方法,光延同样的路径返回,所以地球相对于以太的速度对双程时间的影响取决于地球速度与光速之比的平方(v2/c2),这个量太小了,难以观测。” 1887年,迈克尔逊设计出了一种方案,利用相互垂直的两束光产生干涉的方法来比较光速的差异。假设以太风是在横向的,则横向光束传播一个来回需要用时和在纵向光束传播一个来回需要用时有差别。由此可计算出光产生干涉条纹移动的预期值。但他所观察到的条纹移动远远小于预期值。这个实验结果是对静止“以太”理论的一个挑战。 在1889年时,奥利弗希维赛德(Oliver
Heaviside)从麦克斯韦方程组(Maxwell's
equations)的磁矢势场(magnetic
vector potential field)的运动推导出一种可能的解决办法,即:因子
在1899-1904年期间,由于迈克尔逊- 莫雷实验(Michelson-Morley experiment)的零结果,洛伦兹不得不用“v/c”的概念来解释他的理论,这最终形成了数学方法的洛伦兹变换(Lorentz transformation)。1904年,洛仑兹提出:通过以太的运动物体,纵向线度发生收缩(平行运动方向),其收缩的比例恰好使以太流的影响被抵消。这一假说称为收缩假说[4],由洛伦兹和斐兹杰惹所提出。根据他的设想,观察者相对于以太以一定速度运动时,长度在运动方向上发生收缩,抵消了不同方向上由于以太所造成的光速差异,这样洛仑兹就在不抛弃以太概念的前提下解释了迈克尔逊-莫雷实验的结果。其理论公式如下:
在1905年,昂利•庞加莱(Henri Poincare)发表了他的第一篇关于相对论的论文。该论文的课题是「部分运动学的,部分动力学的」,并包括洛伦兹关于洛伦兹变换(实际上是庞加莱给它这个名字的)的证明的更正。庞加莱实际比爱因斯坦的工作更早一步,并起草了一个狭义相对论的简略版。在1898年,在「时间的测量」中,他阐述了相对论原理,根据这个原理,没有机械或电磁试验可以区分匀速运动的状态和静止的状态[5]。和荷兰理论家洛伦兹的合作中,他把时间的物理推向极限来解释快速运动的电子的行为。在1909年,洛伦兹也对此作了相似的理论阐述[6]。 洛伦兹因子的最终形式 1900年,庞加莱指出:迈克尔逊- 莫雷实验结果表明在“以太”中的绝对运动和相对运动的形式是无法区别的,并首先提出了“相对运动原则”和“相对空间”的观点。对此,在1904年,洛伦兹发表了一篇重要文章来解释他的理论,指出电磁场的作用是独立于整个运动体系的[7]。 1905年,庞加莱指出电磁场的洛伦兹方程不能满足洛伦兹协变性或洛伦兹共变性(Lorentz covariance)。通过使用变换群属性(“群公理”),他证明了麦克斯韦-洛伦兹方程组(Maxwell-Lorentz equations)的洛伦兹协变性。由此,庞加莱推导出了洛伦兹因子的最终形式[8]:
洛伦兹因子的意义 从上述的考证过程中可以了解到:最初的意义上的洛伦兹因子是基于以洛伦兹为代表的“以太”理论推导的。洛伦兹他们一生都没有放弃“以太”理论。庞加莱在1900年就指出:“以太”是协调洛伦兹变换和牛顿第三定律所必须的;在1912年他发表的“量子理论”一文中,他曾十次提到“以太”,并认为光就是“以太”发光的振荡(luminous vibrations of the ether)[9]。
【结果及讨论】 洛仑兹(H.A.Lorentz)提出了一个假设,认为一切在以太中运动的物体都要沿运动方向收缩。由此他证明了,即使地球相对以太有运动,迈克尔逊也不可能发现它。爱因斯坦从完全不同的思路研究了这一问题。他指出,只要摒弃牛顿所确立的绝对空间和绝对时间的概念,一切困难都可以解决,根本不需要什么以太。 最终,阿尔伯特•爱因斯坦重建了整个物理大厦,是他推出了成功的新相对性的模型。他和赫尔曼•闵可夫斯基发展了相对论。赫尔曼•闵可夫斯基(Hermann Minkowski,1864年6月22日-1909年1月12日),德国数学家,犹太人,四维时空理论的创立者,曾经是著名物理学家爱因斯坦的老师。1905年,爱因斯坦在抛弃以太、以光速不变原理和狭义相对性原理为基本假设的基础上建立了狭义相对论。狭义相对论认为空间和时间并不相互独立,而是一个统一的四维时空整体。在狭义相对论中,整个时空仍然是平直的、各向同性的和各点同性的。结合狭义相对性原理和上述时空的性质,也可以推导出洛仑兹变换。
由于相对性原理,变换应该是线性的。 它应该满足光速不变原理。
L-变换是相对论时空观的具体体现。当v<<c时,L-变换G-变换。 【结论】 当今,洛伦兹变换已经成为狭义相对论的代名,“尺缩”和“时慢”完全来自洛伦兹变换的推导,因为它和狭义相对论有同样的数学形式,实验上是无法区分洛伦兹变换和狭义相对论在理论上的区别的。然而,它们之间是有区别的,并且有着本质的区别,那就是洛伦兹变换是基于“以太”尚没有办法测出的假设(或基础)上,只是这种“测不出”正好与狭义相对论吻合,以至狭义相对论时常掩盖了洛伦兹变换的原始思想观点,当然,相对论的时空观和广义相对论的形成也是重要原因。 【参考文献】 1.Born, Max (1964), Einstein's Theory of Relativity, Dover Publications, ISBN 0486607690 2.http://en.wikipedia.org/wiki/Lorentz_ether_theory 3.Darrigol, Olivier (2005), "The Genesis of the theory of relativity", Séminaire Poincaré 1: 1–22 4.Darrigol, Olivier (2000), Electrodynamics from Ampére to Einstein, Oxford: Clarendon Press, ISBN 0198505949 5.Poincaré, Henri (1898/1913), "The Measure of Time", The foundations of science, New York: Science Press, pp. 222–234 6.Lorentz, Hendrik Antoon (1909/16), The theory of electrons and its applications to the phenomena of light and radiant heat at the Internet Archive, Leipzig & Berlin: B.G. Teubner 7.Lorentz, Hendrik Antoon (1892/1907), "Die relative Bewegung der Erde und des Äthers", Abhandlungen über Theoretische Physik, Leipzig: B.G. Teubner, pp. 443–447 8.http://en.wikipedia.org/wiki/Henri_Poincar%C3%A9 9.Poincaré, Henri (1901a), "Sur les principes de la mécanique", Bibliothèque du Congrès international de philosophie: 457–494 . Reprinted in "Science and Hypothesis", Ch. 6-7.
|
|||||||||||||||||||||
| 昂利•庞加莱,法国最伟大的数学家之一,理论科学家和科学哲学家。庞加莱被公认是19世纪后和20世纪初的领袖数学家,是继高斯之后对于数学及其应用具有全面知识的最后一个人。昂利•庞加莱和阿尔伯特•爱因斯坦在他们在相对论上的工作有一段有趣的关系──实际上可以说是缺乏关系(Pais, 1982年)。他们的交互开始于1905年,当时庞加莱发表了他的第一篇关于相对论的论文。该论文的课题是「部分运动学的,部分动力学的」,并包括洛伦兹关于洛伦兹变换(实际上是庞加莱给它这个名字的)的证明的更正。大约一个月后,爱因斯坦发表了他在相对论上的第一篇论文。两人都继续发表相对论上的工作,但是没有任何一个引用对方的工作。爱因斯坦不仅不引用庞加莱的工作,他也宣称从未读过!(不知道他是否最终读过庞加莱的论文。)爱因斯坦最后引用了庞加莱并且承认了他在相对论上的工作,这是在1921年称为「Geometrie und Erahrung」演讲稿中。在爱因斯坦其后的生涯中,他评论庞加莱为相对论的先驱之一。在爱因斯坦死前,爱因斯坦说:“洛伦兹已经认出了以他命名的变换对于麦克斯韦方程组的分析是基本的,而庞加莱进一步深化了这个远见……” | |||||||||||||||||||||